Hidden Subsets

Hidden Subsets are groups of numbers that are "hidden" because they are the only possible candidates in a specific set of cells within a house (a row, column, or block). Once you find them, you can remove all other possible candidates from those cells.

Hidden Pair ✌️

A Hidden Pair is when two numbers can only go in two specific cells within a house. You can then eliminate all other candidate numbers from those two cells.

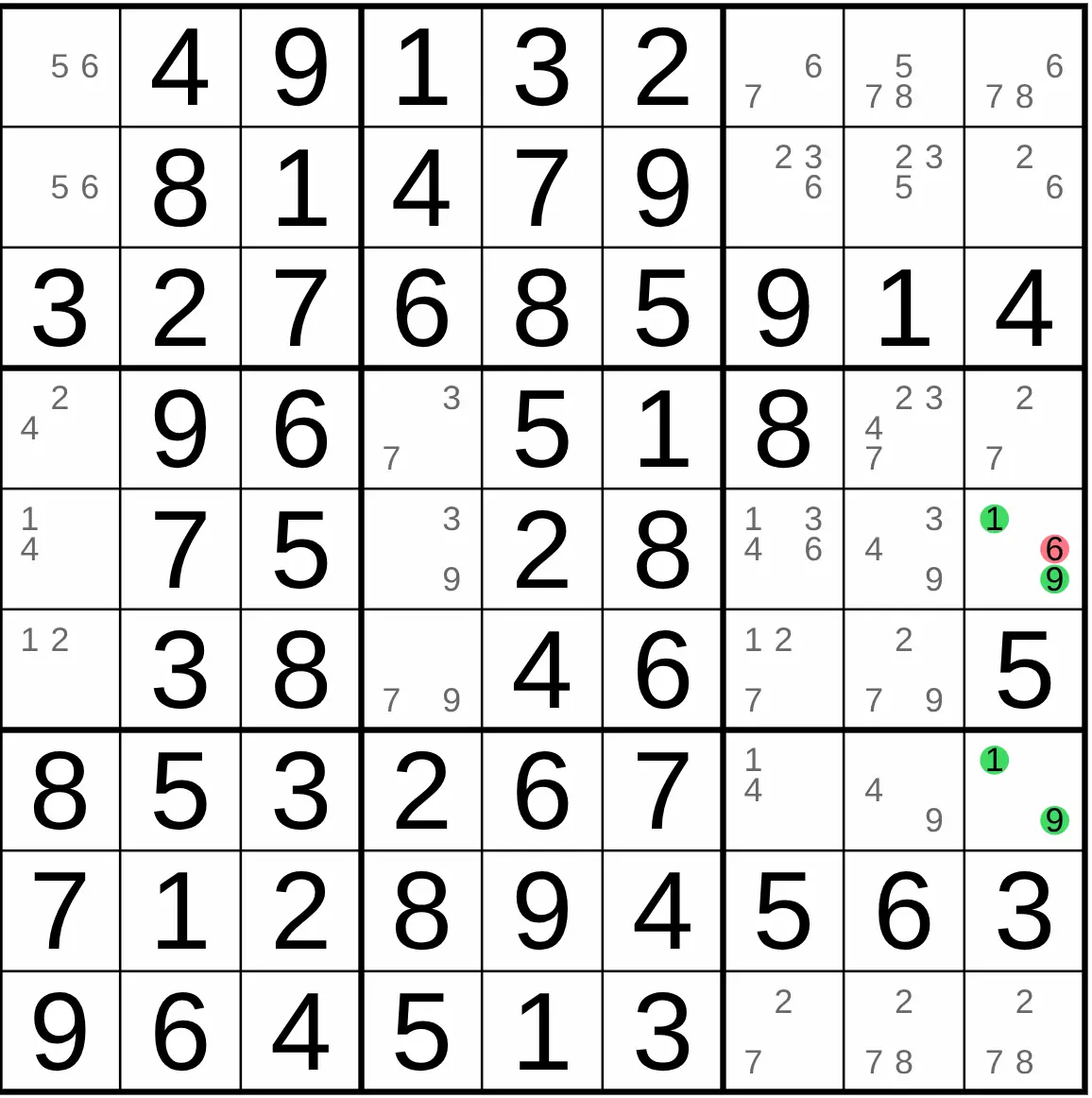
Example: In column 9, the numbers 1 and 9 are only possible in cell r5c9 and r7c9 , even if other numbers are also possible there. You can then remove all other candidates (6 in cell r5c9 of the example above) from those two cells, leaving only 5 and 9.

Hidden Triple 🤟

A Hidden Triple works the same way but with three numbers. When three numbers can only be placed in three specific cells within a house, you can eliminate all other candidates from those three cells. It's important to remember that each of the three cells doesn't need to be able to hold all three numbers; it just matters that those three numbers can't be placed anywhere else in that house.

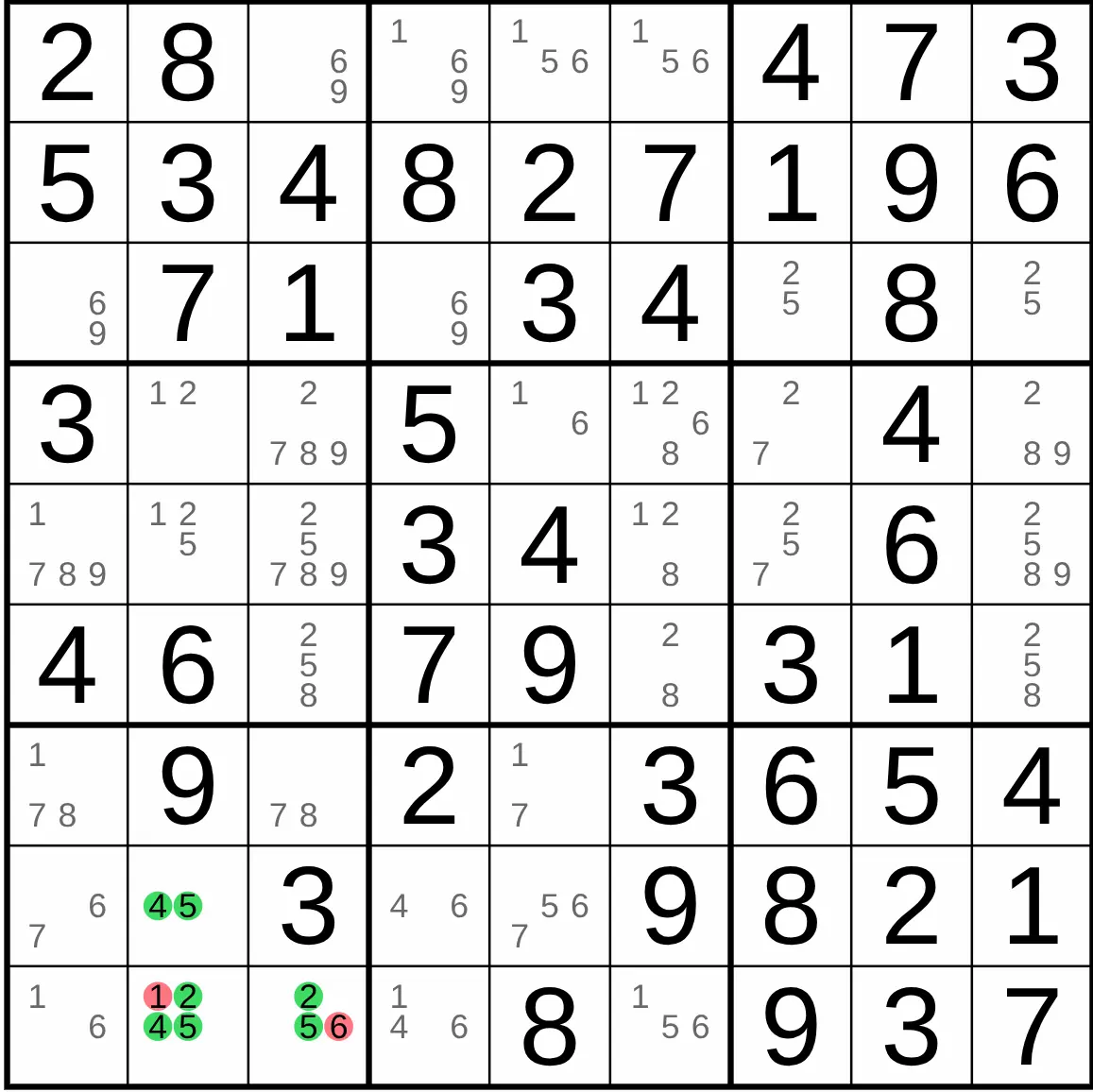
In block 7, the digits 2, 4, and 5 can only be placed in cells r8c2, r9c2, and r9c3. This means you can eliminate the digits 1 and 6 as possibilities from those cells.

Hidden Quadruple 🖖

A Hidden Quadruple is the same principle applied to four numbers. If four numbers can only be placed in four specific cells within a house, you can remove all other candidates from those four cells.

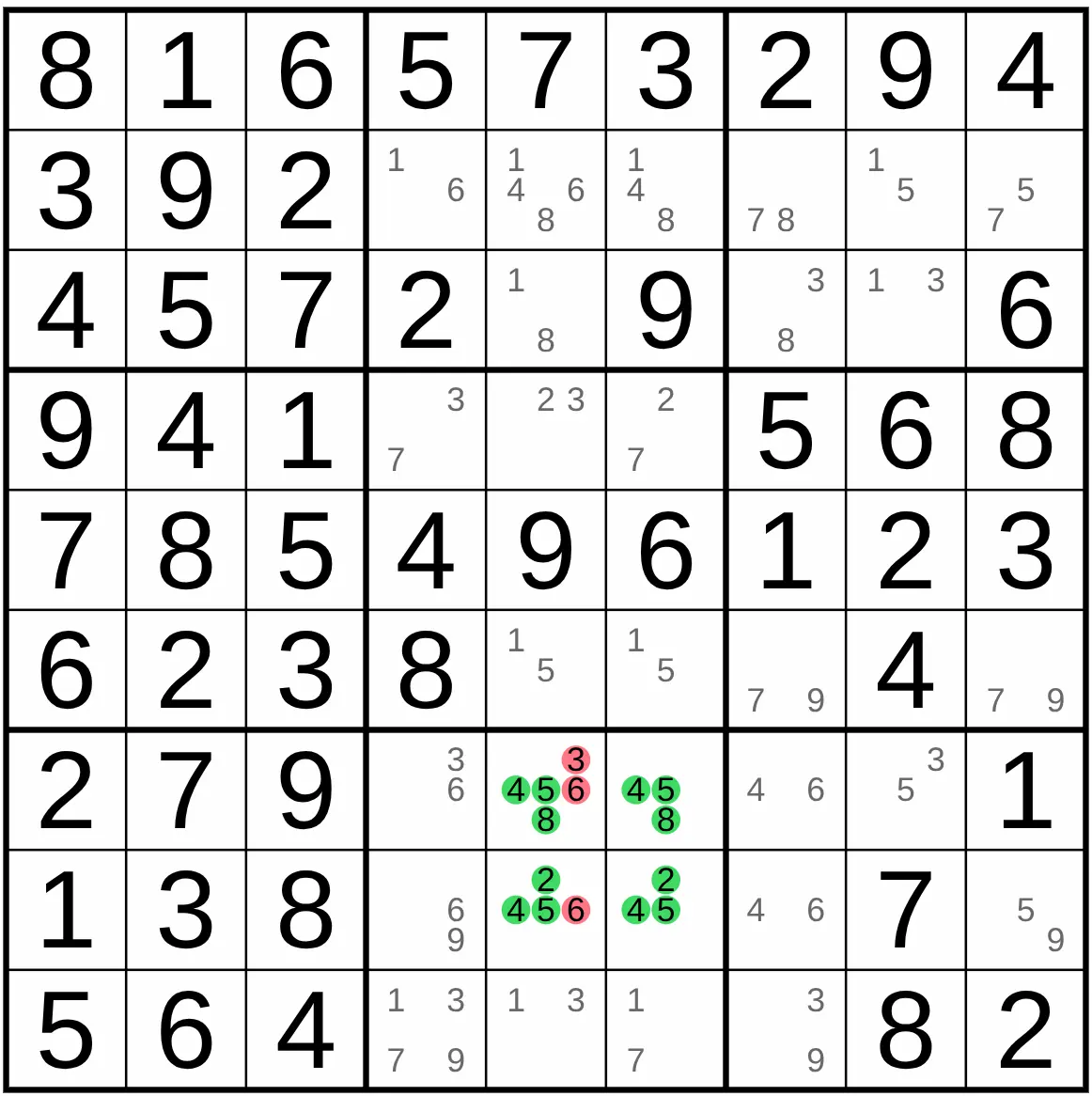
In block 8, the digits 2, 4, 5, and 8 can only be placed in cells r7c5, r7c6, r8c5, and r8c6. These four cells are now a Naked Quadruple, so you know that only those four digits can be placed in them.