Intersections

Here is a simpler, more direct explanation of "Intersections" in Sudoku, and the two types of locked candidates.

The title "Intersections" refers to the core idea behind these two techniques: they both use the intersection of a house (row or column) and a block to eliminate potential candidates. By finding a digit that is "locked" into either a specific row/column within a block or a specific block within a row/column, you can remove that digit as a possibility from other cells.

Locked Candidates: Pointing 📍

If all the possible spots for a digit in a block are lined up in a single row or column, then that digit can't be in any other cell of that row or column outside of that block.

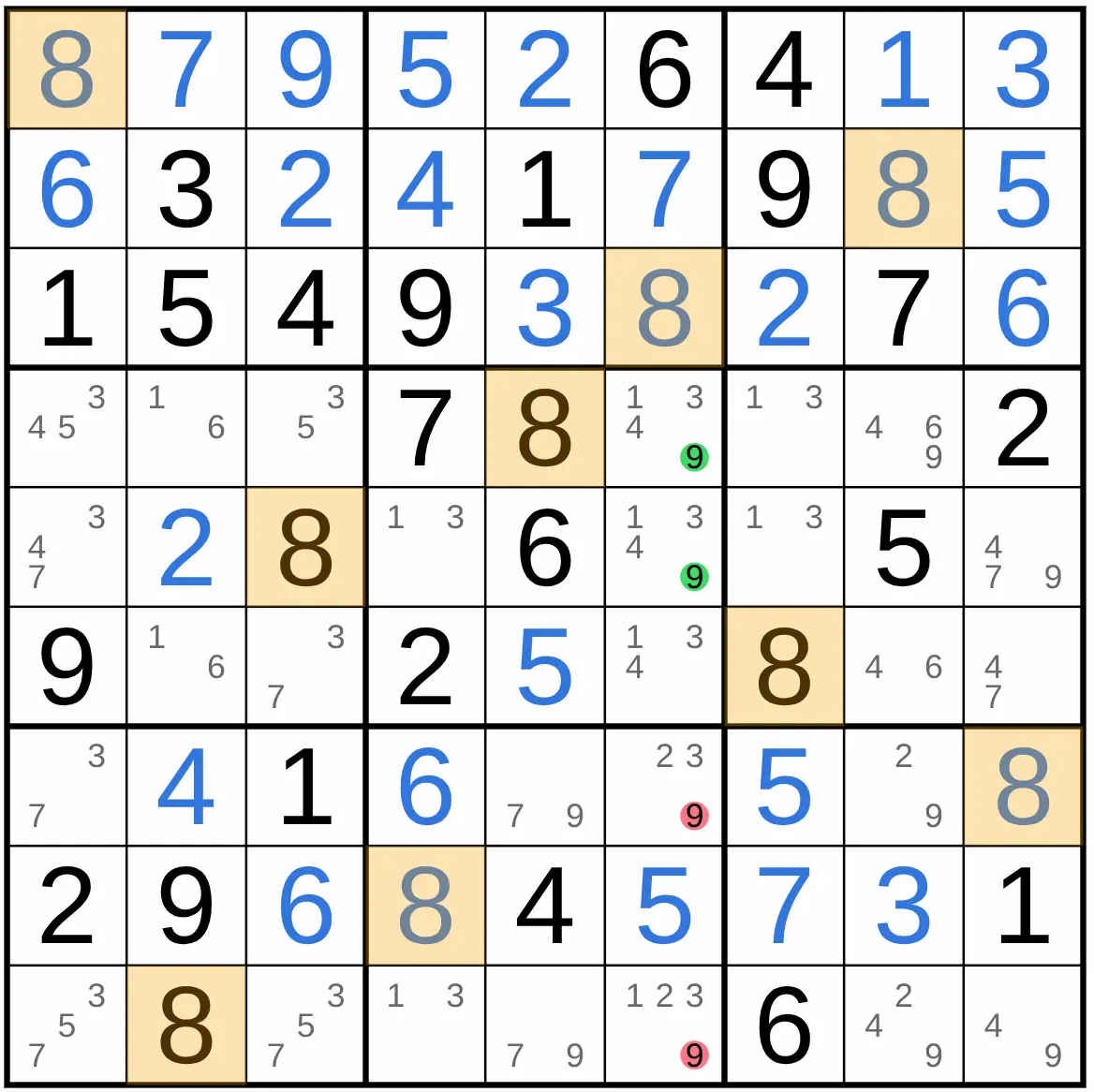
Example: In block 5 only possible places for the digit 9 are in the row 6, so other 9 in row 6 can be eliminate, because block 5 must have a 9.

Locked Candidates: Claiming 🔒

If all the possible spots for a digit in a row or column are located within a single block, then you can remove that digit as a possibility from all other cells within that same block.

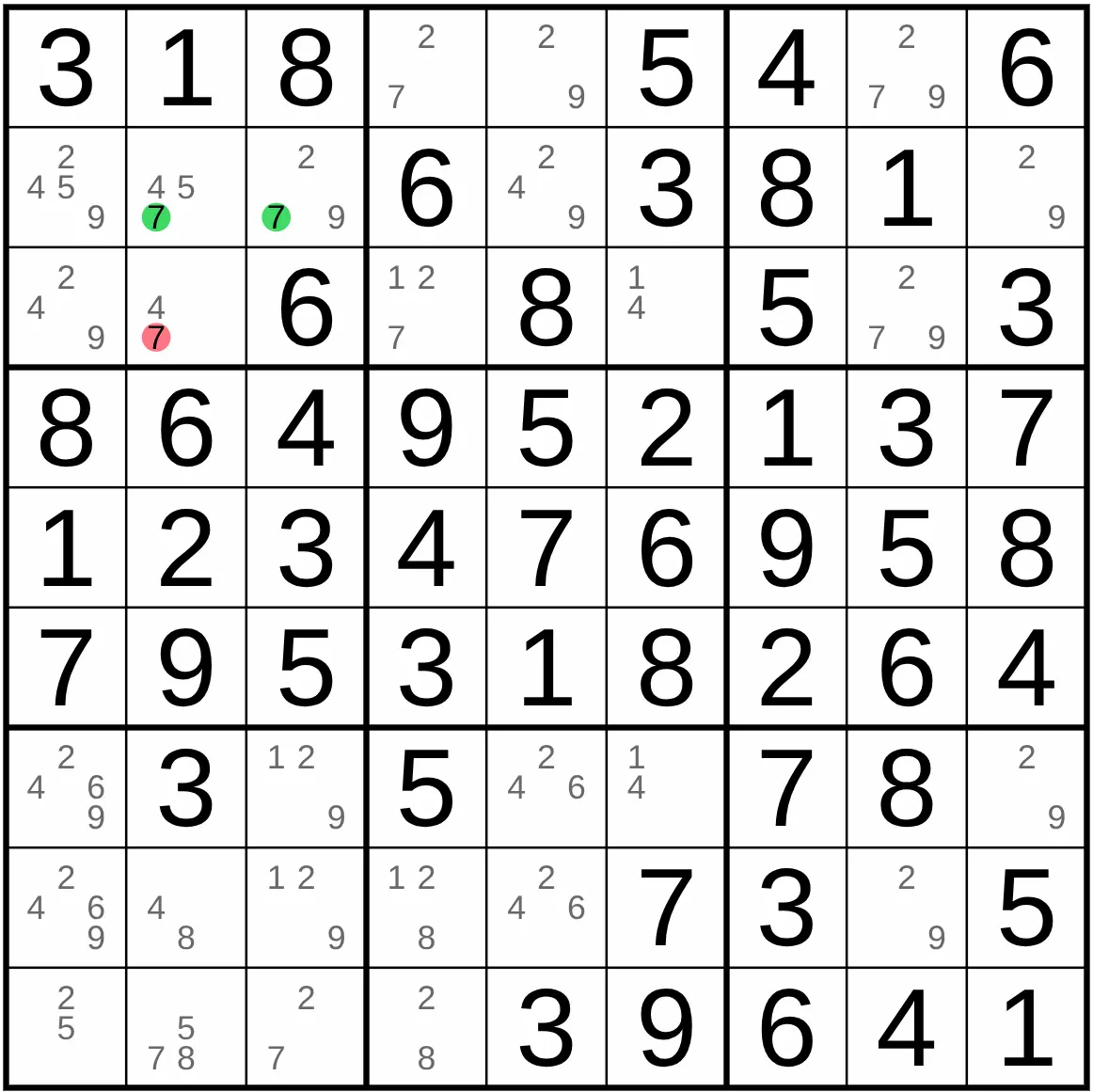
Example: In row 2 only possible places for digit 7 are in the block 1 , other 7 in block 1 can be eliminate